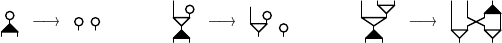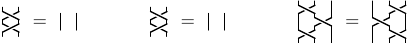Section: Scientific Foundations

Algebraic rewriting

Rewriting theory, in computer science, and combinatorial algebra, in mathematics, are two research fields that share striking similarities: both study the properties of intentional descriptions of complex objects, respectively rewriting systems and presentations by generators and relations. This research direction is devoted to develop a theoretical setting that unifies rewriting and combinatorial algebra, in order to transpose methods of one field to the other one.

Rewriting systems and presentations of algebraic structures have a common generalisation as polygraphs, which are cellular specifications of higher-dimensional categories  [32] . In this setting, we can describe, in a uniform way, different kinds of objects, such as the following ones:

• A rule-based program that computes the list-splitting function used in the merge-sort algorithm:

  Figure 1.

• The usual presentation by generators and relations of the structure of Hopf algebras, containing, in particular, the following relations:

  Figure 2.

• The Reidemeister moves for braids, giving a combinatorial description of those topological objects:

  Figure 3.

More precisely, polygraphs are a common algebraic setting for: abstract, word, term and term-graph rewriting systems  [32] , [36] , [6] and, in particular, first-order functional programs  [39] , [29] , [3] ; set-theoretic operads, pro(p)s, algebraic theories  [36] , [6] ; Turing machines and Petri nets  [36] , [38] , [29] , [3] ; formal proofs of propositional calculus and linear logic  [37] .

In the theoretical setting of polygraphs, the Fox-Squier theory shows that the computational properties of rewriting systems and the mathematical properties of presentations are intimately related to the same topological properties of polygraphs [7] . From this starting point, we progressively establish a correspondence between programs and algebras and we use it to develop applications in different directions:

• Algebraic semantics of programs, such as the new characterisation of evaluation strategies in terms of algebraic resolutions [14] . Here, we want to use well-founded mathematical theories to give a better understanding of programming and, that way, extend the expressiveness of rule-based programming languages.

• Methods from algebraic topology to produce new tools for the static analysis of programs, such as the use of derivations to prove termination and bound computational complexity [6] , [29] , [3] . In this direction, we plan to develop tools from cohomology to classify derivations and, this way, to propose a radically new point of view on computational complexity theory.

• New applications for rewriting, in the field of the formalisation and certification of mathematics, such as the use of rewriting methods to prove coherence theorems or to build resolutions [13] , [14] , [26] .